Технология изучения таблицы умножения и деления с числом 2
1. Изготовление на интегрированном уроке математики и технологии изделий для составления задач и построения их предметных моделей.
В альбоме показано как изготавливаются «Грибочки».
На этом же уроке составляется целая серия задач на умножение числа 2, разделяя грибы по определенному признаку, например, по цвету, по тому, сколько изделий вырезали девочки и мальчики, сколько на одном ряду, сколько на другом, сколько вместе и т. д. Составление задач должно сопровождаться построением моделей. Их решение осуществляется сложением. Если II множитель выражен большим числом, то решение таким способом вызывает затруднение, что и является мотивацией для изучения ТУ числа 2. При проведении уроков, на которых изучается таблица умножения числа на числа 2, 3…10, необходимо учитывать, что наивысшая работоспособность у учащихся вторых классов наблюдается приблизительно с 3 – 4 минуты урока до 15 – 20, и что время перехода информации из краткосрочной памяти – в долговременную составляет около 15 минут. Следовательно, самая главная часть урока, а это анализ составленной таблицы и поиски «узелков на память», должна приходиться на это время.
Цель следующего урока – помочь детям создать таблицу умножения числа 2 и запомнить ее. По типу – это урок изучения нового материала.
Оборудование уроков демонстрационными пособиями показано на рис. 1.

Рис.1. Оформление доски
– Как вы думаете, что мы будем изучать сегодня? (Умножение числа 2). Учитель показывает второй столбик в демонстрационной «Таблице умножения» («ТУ»).
2. Коллективное составление и запись учителем на доске столбика таблицы умножения с использованием «Абака».
Учитель, отодвигая полоску «Абака», открывает 2 кружочка, проговаривает равенство (по 2 взять 1 раз, получится 2) и записывает на доске: 2 • 1 = 2 и т. д. Учащиеся наблюдают, как составляется таблица, и у них появляется желание помочь учителю. Они хором диктуют равенства. На доске получается запись столбика ТУ.
3. Анализ составленной таблицы, поиски «узелков на память».
Учитель берет 2 линейки. Одной ограничивает нужное количество кружочков и соответствующее равенство, а другой манипулирует, руководя тем самым рассуждениями учащихся.
![]() 2 • 1 = 2
2 • 1 = 2
Учащиеся читают хором: «По 2 взять 1 раз, получится 2.
– А если 3 тетради возьмем 1 раз (берет 3 тетради), сколько получится? (3).
– 5 карандашей возьмем 1 раз? (5).
– 100 рублей? (100).
– Какой же вывод можно сделать?
Вывод: если число умножаем на 1, то получается число, которое умножаем. – Откройте «Альбом» на стр. 4 – 5. Давайте хором прочитаем все равенства в первой строке «Таблицы умножения» (1 • 1 = 1, 2 • 1 = 2, 3 • 1 = 3 и т. д.).
– Это правило и будет нашим «узелком на память», когда будем умножать любое число на 1.
– Трудно ли это запомнить? (Нет). Легкие случаи мы будем брать в рамку, то есть обводить со всех сторон (обводит).
![]() 2 • 2 = 4
2 • 2 = 4
Учитель ограничивает 2 полоски с кружочками и равенство 2 • 2 = 4.
Учащиеся читают: «По 2 взять 2 раза, получится 4».
Это учащиеся просто видят, но можно проверить сложением 2 + 2 = 4.
– Как обведем значение произведения? (Со всех сторон).
 2 • 3 = 6
2 • 3 = 6
Учитель ограничивает одной линейкой 6 кружочков, а другой разделяет их на 4 и 2 и говорит: «Нам поможет запомнить произведения 6 сосед сверху – 4». Дети делают вывод, что надо к 4 + 2 = 6.
Значит, это легко вычислить. Ограничим произведение 6 с трех сторон.
2 • 4 = 8 Учитель показывает на «Абаке» 1) 6 + 2 и 2) 4 + 4.
В первом случае учащиеся находят число 8 сложением.
8 ограничивается с трех сторон.
2 • 5 = 10
Показ на «Абаке» выражения 8 + 2 .
Построение пальчиковых моделей.
– Используем "счетную машинку", которая всегда с нами, – говорит учитель, наклоняется и как бы из-под стола достает "счетную машинку" – 2 кулачка, прижатые пальцами друг к другу, и начинает разгибать пальцы по парам.
Выпрямляет мизинцы, постукивает ими друг о друга и в такт говорит:
– По 2 взять 1 раз, получится…(дети хором – 2).
Выпрямляет безымянные и говорит:
-- По 2 взять 2 раза, получится…(4) и т. д.
Повторяя случаи 2 • 1; 2 • 2; 2 • 3; 2 • 4, учащиеся закрепляют их и узнают, что 2 • 5 = 10.
Затем дети, используя свои «счетные машинки», строят модели и хором проговаривают.
– Как обведем произведение 10 в нашей таблице? (Со всех сторон).
– Равенство 2 • 5 = 10 будет главным "узелком на память", потому что поможет узнать соседей.
Учитель складывает две руки ладонь к ладони, прячет большие пальцы внутрь и говорит:
– Если 2 • 5 = 10, то 10 – 2 = 8, т. е. мы узнали еще один способ как найти значение выражения 2 • 4.
– Итак, мы нашли «узелки на память» в первой половине столбика ТУ числа 2. Это случаи 2 • 1 = 2, 2 • 2 = 4, 2 • 5 = 10.
Для запоминания второй половины столбика ТУ числа 2 будем опираться на знание произведений первой.
2 • 6 = 12
Одной линейкой учитель ограничивает на «Абаке» 12 кружочков (6 рядов) и равенство, а другой – разделяет их на 10 и 2.
– Как вы думаете, могут ли нам помочь произведения первой половины столбика, запомнить произведения второй его половины и как? (Да, можно использовать 2 «узелка на память» 2 • 5 = 10 и 2 • 1= 2, к 10 прибавить 2, получится 12).
Учащиеся в паре строят предметную модель на пальцах рук. Ученики первого варианта расправляют кулачки, то есть сразу все пальчики и говорят: « По 2 взять 5 раз, получится 10», а второго – выпрямляют мизинцы, приставляют их к пальчикам соседа и дополняют: «А по 2 взять 6 раз, получится 12». Это легко посчитать. Произведение 12 ограничивается с трех сторон.
2 • 7 = 14
Учитель ограничивает 14 кружочков и разделяет их на 10 и 4. Учащиеся объясняют, что надо 2 • 5 = 10 и 2 • 2 = 4, а всего получится 14. Показывается модель на пальчиках. Ученики первого варианта расправляют кулачки и говорят, по 2 взять 5 раз, получится 10, а второго – приставляют к пальцам соседа мизинцы и безымянные и дополняют: «А по 2 взять 7 раз, получится 14».
Это равенство нам помогут запомнить, 2 «узелка на память» из первой половины столбика 10 и 4, но они расположены далеко от 14. Это трудный случай умножения. Его обозначим с двух сторон (уголком).
2 • 8 = 16
Аналогично строятся модели при помощи «Абака» 2 • 5 = 10 и 2 • 3 = 6 и на пальцах.
Но это произведение запомнить еще труднее, потому что 6 пока не совсем твердо усвоено нами, поэтому ограничим произведение 16 тоже уголком.

– Как вы думаете, какое из двух оставшихся равенств, запомнить легче? – спрашивает учитель (Последнее).
2 • 10 = 20
– Постройте модель этого выражения на пальчиках.
Один ученик раскрывает кулачки и говорит: «По 2 взять 5 раз, получится 10», и другой приставляет кулачки, раскрывает их и добавляет: «А по 2 взять 10 раз, получится 20».
– Откройте «Альбом» (с. 4-5). Прочитаем последнюю строку «Таблицы умножения».
Учащиеся хором называют равенства: 1 • 10 = 10, 2 • 10 = 20, 3 • 10 = 30 и т. д.
Делается вывод, чтобы получить произведение от умножения любого числа на 10, нужно приписать к этому числу ноль.
Это легко запомнить? (Да). Обводим 20 с четырех сторон.
2 • 9 = 18
2 • 10 = 20, а 2 • 10 – 2 = 18.
Учитель закрывает 2 нижних кружочка «Абака» и спрашивает: «Значит, сколько будет, если по 2 взять 9 раз? (18). Строим модель на пальцах.
Ограничиваем это произведение с трех сторон.
Запись на доске приобретает следующий вид (рис. 2):
Рис. 2. Предметная и знаковая модель умножения числа 2 с обозначениями.
Как видим, при запоминании столбика ТУ мы, прежде всего, опирались на взаимосвязь, взаимоотношения между произведениями в нем, то есть на распределительное свойство умножения, с которым учащиеся знакомились в процессе построения предметных моделей (кружочков «Абака»).
Опираться напереместительное свойство умножения, можно только при анализе равенства 2 • 1 = 2, потому что оно входит в ТУ умножения чисел на 1, которую учащиеся усвоили.
Хочется обратить внимание на то, что ранее (это отражено в наших статьях и методических указаниях к комплекту «Таблицу умножения учим с увлечением») при анализе равенств второй половины столбика ТУ мы рекомендовали для запоминания разные варианты. Например, 2 • 8 это –
2 • 5 + 2 • 3; 2 • 4 + 2 • 4; 2 • 6 + 2 • 2; 2 • 7 + 2 • 1. Это приводило к перегрузке памяти, отвлекало внимание детей, занимало драгоценное время. Поэтому советуем для запоминания опираться на умножение числа на 5 и прибавление произведения, полученного от умножения этого числа на числа первой половины десятка, например, 3 • 7 = 3 • 5 + 3 • 2.
4. Подведение итогов запоминания.
– Какие равенства вы хорошо запомнили? – спрашивает учитель.
( 2 • 1 = 2, 2 • 2 = 4, 2 • 5 = 10, 2 • 10 = 20)
– Какие вспомните, немного подумав?
(2 • 3 = 6 , 2 • 4 = 8 , 2 • 6 = 12, 2 • 9 = 18)
– Сколько трудных? Назовите их.
(2 • 7 = 14, 2 • 8 = 16)
Запись на доске:

5. Проверка и закрепление составленной таблицы.
Учитель стирает с доски значения произведений, оставив обозначения, называет и показывает произведения чисел, а учащиеся хором называют их значения.
Отвечать нужно обязательно хором, так как, даже если ребенок еще не уверен в своих знаниях, у него в сознании не успеет зафиксироваться мысль о том, что он не знает. Это очень важный психологический момент в процессе познания.
Путем постановки вопросов учитель побуждает учащихся следить за нитью его мыслей, наталкивает на рассуждения. Можно предупредить детей: «Я вас жалею, и поэтому сначала буду предлагать найти значения более легких выражений, которые затем помогут вам найти значения более трудных. Когда будете играть в «Школу», старайтесь поступать так же».
Например, сначала 2 • 5, затем 2 • 4 или 2 • 6.
Физкультминутка «Отправляемся в плавание».
Учащиеся становятся в круг и берутся за руки. Поют припев и, подпрыгивая, бегут по кругу. Припев:
Мы пришли на бережок –
Поплывем сейчас, дружок,
Чтоб ребят не растерять,
Нужно всех их сосчитать.
На последнем слове припева «сосчитать» они останавливаются и поворачиваются лицом в круг.
Учитель поет запев: «Отправляться в путь пора,
Сядем по два, детвора».
Он являются сигналом к перестроению. Ученики разбираются по два и приседают. Кто остался без пары, руководит счетом. Он взмахом руки поднимает пары по порядку и дети хором считают: «Два, четыре …. шестнадцать». Затем ведущий считает количество двоек, и называет выражение: «По два взять восемь раз, получится…». Дети хором: «Шестнадцать».
Ученики в парах берутся за руки крест-накрест, подпрыгивая, бегут по кругу и поют припев.
Содержание следующего запева является командой для перестроения, например, по тройкам. Дети опять перестраиваются, приседают и считают 3, 6,…. 18, а затем бегут по большому кругу.

Перестраиваясь по четверкам, пятеркам и т д., можно образовывать кружочки, звездочки и, исполняя припев, бежать по малому кругу.
После первого куплета исполняется еще любые 2-3 куплета. Если на названное число ТУ еще не изучалась, то счет ведется только присчитыванием.
6. Самостоятельная работа. Составление таблицы умножения числа 2 в «Волшебной тетрадочке».
Из листа альбома (с. 9, 10) дети отрезают (или надрезают) дополнительный материал. Остается второй листочек «Волшебной тетрадочки».
Построение знаковой модели по предметным картинкам (туфелькам) и образцу. Чтобы легче было ориентироваться, туфельки окрашены в принятые нами цвета. Так, при составлении выражения, учащиеся видят, что рассматриваемая предметная модель заканчивается оранжевыми туфельками, следовательно, по 2 надо взять 3 раза. В процессе изучения таблицы умножения числа 2 необходимо опираться на понятие «пара», употребляемое детьми в житейских ситуациях.

7. Запоминание произведений по месту их расположения в натуральном ряду чисел (в домике «Города умножения»).
а) Построение домика. Работа с диском (если есть возможность). Выполняется задание с помощью компьютерной программы.
б) Определение места расположения произведений в домике демонстрационной таблицы «Город умножения» и этой же таблицы в альбоме (с. 3).
– В каком домике живут произведения от умножения числа 2? (В двухэтажном, красном.)
Учитель показывает его в «Городе умножения» и отдельно в увеличенном виде. Он обводит по воздуху или ограничивает картонным уголком первый прямоугольник и говорит: «По 2 клеточки взять 1 раз, получится…(дети дополняют 2). Произведение 2 живет во второй квартире».

Учитель ограничивает 2 прямоугольника. Учащиеся хором составляют равенство: «По 2 клеточки взять 2 раза, получится 4».

– Где живет произведение в домике? (В четвертой клетке).
Учитель показывает 3 прямоугольника в домике.

Произведение располагается в шестой клетке и т. д.
Таким образом, изучается графическая модель. Необходимо отметить, что этажи располагаются как в Подземном царстве – сверху вниз. Произведения 12, 14….20 расположены на втором этаже домика. А получаются они так: на первом этаже 2 • 5 плюс на втором – 2 • 1, получается 12; 2 • 5 + 2 • 2 = 14.
Причем, надо обратить внимание, что 12 находится под 2, 14 под 4 и т. д. Учащиеся вспоминают, что при работе с «Абаком» они пользовались этим способом запоминания.
Эта закономерность прослеживается во всех четных домиках, когда число умножается на числа второго пятка. Например, при умножении числа 4 на 6 произведение 24 находится в четвертом подъезде, то есть под 4; 28 под 8 и т. д.
в) Учащиеся находят в альбоме (с. 3) красный домик в «Городе умножения», и, поочередно нажимая указательным пальцем на черные точки, хором называют произведения 2, 4, …20.
Работа с домиком «Волшебной тетрадочки».
Игра «Музыканты». Дети нажимают на кружки пальцами левой руки, начиная с мизинца, и хором называют произведения, расположенные на первом этаже (2, 4, 6, 8, 10); пальцами правой руки, начиная с большого пальца, нажимают на кружки второго этажа и называют произведения – 12,14, 16, 18, 20.
Таким образом, для улучшения запоминания мы подключаем моторику. Ведь недаром В. Сухомлинский говорил, что способности ребенка, расположены на кончиках его пальцев.
в) Запись произведений в домике «Волшебной тетрадочки».
Учащиеся, проговаривая про себя выражение по 2 взять 1 раз, записывают его значение – 2 в первый кружочек домика под цифрой 2; проговаривают по 2 взять 2 раза и видят, что 4 записано во втором кружочке под цифрой 4 и т.д.
8. Использование созданных в «Волшебной тетрадочке» моделей для а) взаимопроверки (игра «Школа»), б) самопроверки и оценки знаний.
а) Ученики I варианта выступают в роли «учителей», а II – «учеников». По сигналу учителя (звон колокольчика) начинается мини урок. «Учитель» показывает выражение в столбике, например, 2 • 3 = (полоска с ответами подогнута), а «ученик» – его значение 6 в домике. Если «ученик» ошибся, то «учитель» должен подсказать «узелки на память», и через несколько заданий повторить это выражение. Так что «ученик» все равно получит «улыбку» смайлика, которой его оценит «учитель». Это позволяет раннему выявлению ошибок и их исправлению.
б) Учащиеся из дополнительного материала вырезают розовую полоску со смайликами, накладывают ее между знаком равно (=) и линией сгиба так, чтобы смайлики были ниже клеток тетрадочки (см. обложку «Альбома»), загибают сверху полоску за листочек и сбоку подгибают вниз тетрадную полоску со значениями выражений. Дети пишут значения выражений на розовой полоске, отгибают ответы справа, проверяют по идеальному образцу и оценивают свою работу при помощи смайликов. Если все правильно, то смайлик с выражением на лице «огорчения» подгибается вниз, и остается смайлик - «радость». Если допущена ошибка, то ученику надо подсказать «узелки на память» и дать полоску, вырезанную из тетрадного листа в клетку, на которой он должен повторить работу. У учителя на всякий случай должны быть эти полоски. Хотя случаев этих почти не случается.
На этом технология прерывается. На протяжении всего урока учащиеся видели таблицу умножения числа 2 по порядку.
Дома дети могут поиграть в «Школу», сами себя проверить, придумать задачи.
На следующем уроке
9. Запись вперемешку ТУ числа на второй странице «Волшебной тетрадочки». Взаимопроверка (игра «Школа»), самопроверка и оценка знаний
Учащиеся открывают вторую страницу этого же листочка «Волшебной тетрадочки» и поворачивают ее так, чтобы верх оказался внизу, а линия сгиба – справа.

· Выделение квартир для произведений. Дети ставят в домике 10 точек там, где должны жить произведения.
· Заселение домика. Например, первым приехало число 12. Оно записывается во второй клетке второго этажа. Скучно ему в пустом домике, пошло оно погулять по дорожке, остановилось вверху и к нему прибежали его множители – 2 • 6. Затем приехало в домик, например, 8. Оно записывается в восьмой клетке первого этажа и т. д. Таким образом, будет записана таблица умножения числа 2, причем, ни одно равенство не будет пропущено и ни одно не повторено дважды.
· Взаимопроверка. Игра «Школа».
· Самопроверка.
10. Цветовое кодирование информации.
а) Работа с диском. Выполнение программы к «Цветовым кодам».
б) Нахождение произведений, полученных от умножения изучаемого числа, среди других произведений в демонстрационной «Таблице с цветовым кодом». Игра «Хлопки». Проверка по цветовым кодам.

Учитель напоминает правила игры: «Я буду показывать числа по порядку, вы должны хлопнуть в ладоши тогда, когда увидите число, полученное от умножения числа 2. Он закрывает линейкой коды первого ряда, показывает число 1. Дети не хлопают (хотя кто-то из учащихся может и хлопнуть, потому что при изучении умножения числа 1 хлопали подряд). Учитель отодвигает линейку, дети видят, что там нет красного кода. Он показывает число 2, дети хлопают, линейка отодвигается и открывается белый и красный код. Учитель показывает 3, дети не хлопают, линейка отодвигается, и они видят, что на первом месте стоит белый код, на третьем – оранжевый, а на втором месте красного кода нет, значит, это число не является значением произведения от умножения числа 2. Таким образом, учащиеся хлопают 10 раз. Они также замечают, что значения произведений расположены в данной таблице также как в домике, то есть на двух этажах.
в) Работа в паре с «Таблицей с цветовыми кодами» (с. 3 обложки альбома). Игра «да – нет». Один ученик закрывает коды и показывает вперемешку произведения. Другой ученик, если это произведение от умножения числа 2, шепотом говорит: «Да», если другое: «Нет».
11. Проверка знания каждым учащимся каждого равенства столбика ТУ при помощи «Цветовой сигнальной ленты» и «Цветовых сигнальных карточек».
На доске рядом с «Цветовой сигнальной лентой» (цвета расположены вперемешку) записываются по порядку (чтобы легче было искать) числа 4, 6, 8….18. Учитель показывает таблицу «Город умножение» и говорит: «Если вы хорошо усвоили таблицу умножения числа 2, то сможете перейти дорогу от домика № 2 к домику № 3». Он называет, например, выражение по 2 взять 5 раз. Ученики видят, что его значение – 10 написано, например, рядом с желтым цветом и показывают «Цветовую сигнальную карточку» желтого цвета. Учитель обводит число 10 кружочком, это значит, что можно идти дальше и т.д.
Таким образом, за 1 минуту проверяется усвоение каждым учеником каждого равенства изученной таблицы умножения числа 2.
12.Подведение итогов. Работа с индивидуальной и демонстрационной «Таблицей умножения».
Учащиеся дорисовывают «улыбку» в смайликах над вторым столбиком равенств в «Таблице умножения», расположенной в альбоме (с. 4-5).
Вывешивается «Таблица умножения» учитель закрывает значения выражений во втором столбике, называет по порядку выражения, а ученики хором – их значения. Подводится итог, что таблица умножения числа 2 усвоена.
Технология изучения деления по содержанию
В старину умножение считалось нелегким делом, а уж деление тем более. В Италии существует поговорка «Трудное дело деление». Было придумано немало методов деления. Мы пользуемся сейчас арабским способом деления, основанным на позиционной десятичной системе счисления, получившим название «золотое деление».
Формирование понятий о делении по содержанию и делении на равные части осуществляется в процессе построения предметных, графических и знаковых моделей (с. 9 – 14 «Альбома»).
Построение предметных моделей.
Коллективная работа. Составление задач с использованием грибочков.
1. «3 мальчика нашли по 2 грибочка. Сколько всего грибов собрали дети?»
К доске вызываются 3 мальчика. Они прикрепляют к доске грибочки по отдельности. Составляется равенство, и грибочки объединяются.
2. «Дети собрали 6 грибочков и положили их по 2 в корзинки. Сколько корзинок понадобилось им?»

Грибочки разъединяются и рисуются корзинки.
Совершаемые действия сопровождаются проговариванием: по 2 грибочка взять 3 раза, получится 6; 6 грибочков разделить по 2 грибочка, получается 3 раза, значит нужно 3 корзинки.
Составляется несколько аналогичных задач только на деление.
Необходимо обратить внимание на то, что в записи равенств на умножение и деление бывает только 2 одинаковых наименования и провести сравнительный анализ с равенствами на сложение и вычитание.
Построение моделей задач по предметным картинкам.
Учитель говорит: «12 туфелек нужно упаковать по паре в коробки. Сколько потребуется коробок?» Ограничьте модель этой задачи в «Волшебной тетрадочке» и покажите ответ при помощи «Цветовой сигнальной карточки». Дети показывают карточку голубого цвета (6) и т.д.
Построение графических моделей.
Учащиеся вырезают из «Альбома» красную полоску, складывают ее гармошкой. Учитель называет выражение, например, по 2 квадрата взять 4 раза, просит растянуть гармошку и показать его модель. Учащиеся показывают, полоску, равную 8 квадратам. На доске записывается равенство.

![]()
![]()
2 кв. • 4 = 8 кв. 8 кв. : 2 кв. = 4 (прямоугольника)
Затем называется выражение 8 квадратов разделить по 2 квадрата. Гармошка слегка сжимается. Получилось 4 прямоугольника. Дети переворачивают полоску изнаночной стороной, и видят подтверждение ответа.
Равенства записываются на доске.
Выполняется несколько аналогичных упражнений.
Затем рассматриваются способы измерения площади прямоугольников, данных в «Альбоме», и делается вывод.

Учащиеся измеряют первый прямоугольник гармошки, приложив его к меркам. Вывод: площадь маленьких прямоугольников тоже равна 2 кв. см. Выполняется несколько упражнений на умножение и деление с опорой на меру площади квадратный сантиметр. Например:
2 см2 • 5 = 10 см2
10 см2 : 2 см2 = 5 (прямоугольников).
Модели задач на деление по содержанию можно показать также в таблицах «Город умножения» и «Радужный цветок».
Задачи № 1 и 2, данные в «Альбоме», решаются самостоятельно. Это свидетельствует о том, что полученные знания могут использоваться на практике.
Деление на 2 равные части
Учитель читает сказку «Два жадных медвежонка».
– Почему пострадали медвежата? (Потому что не умели поделить сыр на две равные части и были жадные). Предположим, что медвежата нашли конфеты. Помогите им разделить сладости».
Работа с предметами.
Ученику предлагается разделить 6 конфет на 2 части поровну. Он их раскладывает по одной конфетке поочередно на два блюдца. Получилось по 3 конфеты.
– Предположим нужно разложить 18 яблок в 2 корзины поровну. Удобно ли раскладывать их так же, как конфеты? – спрашивает учитель. (Нет, потому что долго). Поэтому надо знать таблицу деления на 2 равные части.
Это и является мотивацией.
Коллективная работа. Построение предметной и знаковой модели.
Учащиеся вырезают из «Альбома» серые линеечки длиною 20 см. Учитель предлагает им сложить линейки пополам и спрашивает: «На сколько частей вы разделили линейки? (На 2). Чему равна длина каждой части? (10 см).
Учитель с проговариванием (20 см разделить на 2 равные части, получится по 10 см) записывает равенство на доске: 20 см : 2 = 10 см
– Отрежьте 2 см справа. Чему равна длина линейки? (18 см). Разделите ее на 2 равные части.
– Продиктуйте хором равенство (18 см разделить на две равные части, получится по 9 см).
Учитель записывает на доске: 18 см : 2 = 9 см и т.д.


В результате на доске появляется знаковая модель – таблица деления на 2 равные части, а у детей в руках останется линеечка длиною 2 см, сложенная вдвое.
Самостоятельная работа. Составление таблиц деления и умножения на 2.
«Обычно, – говорит учитель, – таблицы записываются, начиная с самого маленького числа.
Опираясь на кружочки «Радужной горки» (с. 10 альбома), учащиеся по выражениям левого столбика находят значения произведений, а правого – значения частных, то есть составляют 2 таблицы.

Рис. 4. Предметно-цветовая и знаковая модель умножения и деления чисел на 2 «Радужная горка»
Самостоятельная работа.
Решаются задачи, данные в «Альбоме»: 1) В одном пакете 4 лимона. Сколько лимонов в двух таких пакетах? 2) 8 лимонов разложили поровну в 2 пакета. По сколько лимонов в каждом пакете?
Учитель должен обратить внимание на связь действий умножение и деление, поэтому он тоже записывает решение на доске.
4 л. • 2 = 8 л. 8 л. : 2 = 4 л.
– Как называется число 8 в действии умножение? (Произведение).
– Как называется число 8 в действии деление? (Делимое).
Это уточнение позволяет нам перейти к следующему этапу работы.
Работа с «Таблицей с цветовым кодом».
Формирование понятия о четных и нечетных числах
Платон говорил, что арифметика есть учение о четном и нечетном.
Когда мы изучали умножение числа 2, то искали в этой таблице произведения. Теперь нам нужно найти числа, которые делятся на 2, то есть делимые.
Игра «Хлопки». Учитель закрывает коды I ряда (этажа) и показывает по порядку делимые.
– 1 делится на 2? (дети не хлопают). Отодвигается линейка – красного кода нет.
– 2 делится на 2? (хлопок). Отодвигается линейка – красный код есть.
– 3 делится на 2? и т. д.
Учитель сообщает, что числа, которые делятся на 2, называются четными, а числа, которые не делятся на 2 – нечетными.
– Какие числа расположены в домике «Волшебной тетрадочки» на I этаже? (Четные). Нажимая пальчиком, назовем их хором (2, 4, 6, 8 и 10).
– Скажите, а числа II этажа делятся на 2? (Да). Значит, они тоже
четные. Назовем и их также (12, 14, 16, 18 и 20).
– Обратите внимание, что все эти числа расположены в четных подъездах (столбиках).
При дальнейшем изучении ТУ нужно сделать вывод, что все числа, которые заканчиваются цифрами 2, 4, 6, 8 и 0 являются четными.
Следует обратить внимание на то, что в домиках «Города умножения», расположенных справа все числа четные, а слева – чередуются четные и нечетные.
Умножение чисел на 2
– Вы уже составили ТУ на 2 по кружочкам «Радужной горки». А сейчас поищем «узелки на память». Как видите, 1 • 2 = 2 мы уже знаем, а второе 2 • 2 = 4 знаем? (Да). Как его можно прочитать?
(Дети читают: «По 2 взять 2 раза, получится 4; 2 умножить на 2, получится 4; первый множитель (множимое) 2, второй множитель 2, произведение 4.)
А какая песенка поможет нам запомнить это равенство?
Учитель напевает или включает запись первого куплета песни В. Шаинского на слова М. Пляцковского «Дважды два – четыре».
Дважды два – четыре,
Дважды два – четыре.
Это всем известно
В целом мире!
– А вам это уже известно? (Да!)
– Эта песенка будет "узелком на память".
– А еще есть поговорка, если человек что-то очень хорошо знает, то он говорит: «Я это знаю, как дважды два – четыре».
Равенство 3 • 2 = 6 можно прочитать так же: дважды 3 – 6. Это значит, что число 3 взяли дважды, то есть 2 раза. Как видим, мы сначала называем второй множитель 2 (дважды), а затем первый множитель (множимое), то есть число, которое умножаем. Давайте так прочитаем всю таблицу (дети читают хором).
Этот вариант чтения закрепляется при умножении на 3 и 4.
При формировании этого понятия можно установить межпредметную связь с уроками чтения. Слово трижды очень часто употребляется в сказках. Например, в конце сказки «Сестрица Аленушка и братец Иванушка» козленочек от радости трижды перекинулся через голову и обернулся мальчиком. Можно спросить у детей: «Из каких копытец хотел напиться Иванушка (из коровьего, лошадиного и козьего)? Сколько раз он спрашивал разрешения у Аленушки, чтобы напиться? (3 раза, то есть трижды).
Для понимания и запоминания умножения на 2 опираемся на имеющиеся у учащихся знания состава чисел I и II десятка.
– Заменим действие умножение сложением:
1 • 2 = 2 1 + 1 = 2; 2 • 2 = 4 2 + 2 = 4; 3 • 2 = 6 3 + 3 = 6 и т. д.
Делается вывод, что при сложении двух одинаковых чисел первого десятка получаются четные числа первого и второго десятка. Они и являются значениями произведений умножения чисел на 2. Эту информацию учащиеся видели на клапанах «Суперпапки» при изучении состава чисел первого и второго десятка.
Это легко запомнить? (Да).
Пособие «Лабиринт» является пространственно-цветовой моделью умножения на 2. Она позволяет создать яркий, понятный и легко запоминающийся образ данной таблицы.
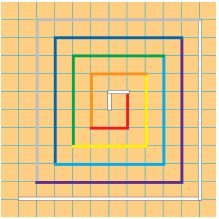
![]()
Учащиеся без особого труда устно составляют таблицу умножения чисел на 2. Определяется ее место в системе знаний – в «Таблице умножения» (с. 4-5 альбома). Дети с радостью находят ее во второй строке. Помогает этому то, что число 2 обозначено красным цветом. Получается, что дети уже знают вторую строку ТУ, то есть еще 8 равенств.
На следующих уроках модель этой таблицы нужно найти и прочитать в двух лепестках «Радужного цветка», оградив их длинной линейкой, в двух нижних строках «Квадрата с уголком» и создать в «Цветике-семицветике».
Деление с частным 2
Для построения предметной модели используются грибочки, изготовленные детьми. Составляются 3 задачи.
1. «2 мальчика нашли по 3 грибочка. Сколько всего грибов собрали дети?»
К доске вызываются 2 мальчика. Они прикрепляют к доске грибочки по отдельности. Составляется равенство, и грибочки объединяются.
2. «Дети собрали 6 грибочков и разложили их по 3 в корзинки. Сколько корзинок понадобилось им?»
Грибочки разъединяются по 3 и рисуются 2 корзинки.
3. Дети собрали 6 грибочков и разложили их в 3 корзинки. По сколько грибочков в каждой корзинке?
Совершаемые действия сопровождаются проговариванием и записью учителем на доске:
1) по 3 грибочка взять 2 раза, получится 6 грибочков;
2) 6 грибочков разделить по 3 грибочка, получается 2 раза, значит нужно 2 корзинки;
3) 6 грибочков разложить в 3 корзины поровну, получится по 2 грибочка в каждой корзине.

Для закрепления понятий деление по содержанию и деление на равные части используется красная полоска. Например, 8 квадратов разделить на 4 прямоугольника, получится по 2 квадрата в каждом прямоугольнике.
Систематизация знаний в процессе изготовление дидактической игрушки «Чудесные превращения»
Завершающим этапом технологии изучения табличного умножения и деления с числом 2 является систематизация знаний. Те понятия и навыки, которые сформированы, учащиеся должны сохранить в материальном виде, в обобщенной знаковой модели «Чудесные превращения". Поворачивая ее грани, можно наблюдать зависимость между компонентами действия умножения и деления и их результатами. В альбоме даны развертки моделей на умножение и деление с числами 2, 3, 4 и 5 (с. 29 – 32).
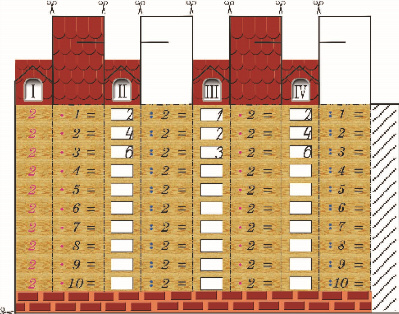
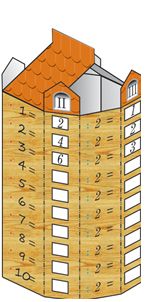
Модель умножения и деления с числом 2
«Чудесные превращения»
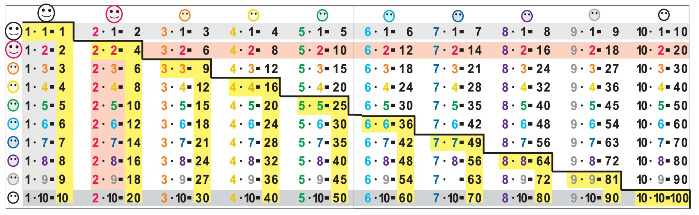
Подсчет количества усвоенных равенств в «Таблице умножения» альбома
После изучения умножения числа 1 и на число 1 было усвоено 19 равенств. Это первый столбик – 10 равенств и первая строка – 9.
После изучения умножения числа 2 и на 2 – 25. Это – 9 равенств второго столбика, 8 – второй строки и 8 – последней.
Всего: 19 + 25 = 44 из 100.
Учащиеся рисуют улыбки в смайликах над вторым столбиком, перед второй и последней строками.
Некоторые учащиеся уже поняли, как получаются произведения от умножения числа 10 , то есть последнего столбика. Однако пока не следует на это обращать внимание всего класса. Лучше сделать вывод при изучении умножения чисел на 3 на основании накопленного опыта: 10 • 1 = 10;
10 • 2 = 20; 10 • 3 = 30 (по 1 десятку взять 3 раза, получиться 3 десятка или тридцать) и т. д.
Выводы и предложения
Таким образом, в процессе построения серии моделей, учащиеся как по цепочке проходят путь развития знания и в результате многократного разнообразного повторения усваивают таблицы умножения и деления с числом 2.
Изучение таблицы умножения по данной технологии на первых порах вызывает у учителей затруднения, связанные с использованием незнакомых ранее пособий, смущает замедленный темп работы. Начало изучения столбика ТУ определенного числа, является началом формирования вычислительного навыка, который должен пройти этапы от действий в замедленном темпе с тщательным обдумыванием каждого движения мысли, до их выполнения в быстром темпе, в свернутом виде, автоматически.
Знание алгоритма способствует ускорению темпа работы при изучении ТУ чисел 3, 4…10 и позволяет сосредоточить внимание на усвоении более сложного содержания учебного материала.
