Согласно требованием программы к концу второго класса должны быть сформированы вычислительные навыки табличных случаев сложения и вычитания однозначных чисел.
Комплексное использование демонстрационных и индивидуальных наглядных пособий обеспечит достижение положительного результата с наименьшими затратами сил и времени как учителя, так и ученика, что является необходимым условием здоровьесберегающих педтехнологий.
Использование пособий в определенной последовательности обеспечивает этапы усвоения информации по формированию понятия о сложении однозначных чисел с переходом через десяток и вычислительных навыков, путем построения предметных (рисунки овощей), графических (кружочки) и знаковых (цифры) моделей.
Благодаря демонстрационным пособиям с подвижными деталями учащиеся имеют возможность увидеть в динамике формируемые понятия и действия сложение и вычитание, а при наличии у детей комплектов индивидуальных наглядных пособий "Математика от 1 до 20. Суперпапка" выполнить эти же действия самим.
Большинство из представленных ранее пособий используется и для изучения чисел второго десятка. Это обеспечивает преемственность в предъявлении содержания учебного материала от простого к сложному и преемственность в последовательности выполнения учебных действий. Ориентиром в этой работе выступит последовательность использования наглядности.
Алгоритм изучения чисел второго десятка
I. Образование чисел от 11 до 20
1. Предъявление образа чисел. Работа с таблицами из демонстрационных наглядных пособий«Сказочный счет».
2. Образование чисел из одного десятка и нескольких единиц. Работа со второй частью демонстрационного и индивидуального наглядного пособия «Линейка «Счет от 1 до 20».
3. Построение предметной модели чисел при помощи «Абака».
4. Построение графической, цветовой и знаковой модели чисел с использованием «Компьютера».
II. Сложение однозначных чисел с переходом через десяток
1. Построение предметной модели задачи при помощи «Абака».
2. Построение ее графической, цветовой и знаковой модели с использованием «Компьютера» и ее преобразование, создание проблемной ситуации.
3. Построение знаковой модели при помощи «Линейки «Счет от 1 до 20». Запись на доске.
III. Состав чисел II десятка
1. Построение графической, цветовой и числовой модели состава чисел. Работа с демонстрационным и индивидуальным пособием «Компьютер».
2. Закрепление знаний. Самостоятельная работа в тетради.
3. Применение полученных знаний на новых информационных полях и в новых ситуациях. Работа с демонстрационными пособиями «Радужная горка» и «Числовая горка».
4. Взаимопроверка знаний. Работа «в паре» с индивидуальными пособиями «Радужная горка», «Числовая горка», «Столбик таблицы сложения однозначных чисел».
5. Проверка знаний учителем. Работа с «Цветовыми сигнальными карточками» и «Цветовой сигнальной лентой».
ТЕХНОЛОГИЯ ИЗУЧЕНИЯ ЧИСЕЛ ПЕРВОГО ДЕСЯТКА
I. Образование числа 11
1 . Предъявление образа числа 11. Работа с таблицами из «Сказочного счета».

а) б) Рис. 1
Иллюстрации к сказкам «Про Козленка, который умел считать до десяти» и «Красная шапочка». Образование числа 11.
Рис. 1 а подсказывает название числа – одиннадцать (дцать – это сокращенное десять), а рис. 1 б, как его образовать. Дети находят число 11 на корпусе парусника и его модель в «Радужной горке» (нижний ряд 1 десяток и 1 белый с точкой шарик вверху).
Аналогично происходит знакомство с числами 12, 13…19.
2. Образование числа 11.
Работа со второй частью «Линейки «Счет от 1 до 20». Сначала учитель, а затем учащиеся устанавливают окошко на своих линейках, как показано на рис. 2, и видят, что если к 10 прибавить 1, получается 11.
 Рис. 2.
Рис. 2.
Линейка «Счет от 1 до 20» II ч. Модель числа 11.
3. Построение предметной модели числа 11 при помощи «Абака» (рис. 3).
По картинкам составляется задача: «В вазе лежало 10 яблок. В нее положили 1 грушу. Сколько фруктов стало в вазе?». Дети хором: 10 + 1 = 11(фр.).
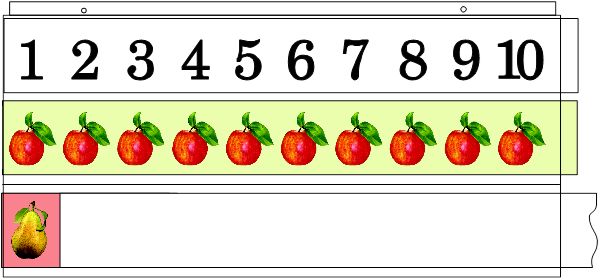
Рис. 3. «Абак». Модель задачи.
4. Построение графической, цветовой и знаковой модели числа 11 с использованием «Компьютера».
Учащиеся, проговаривая, строят модель этой задачи при помощи «Компьютера» (рис. 4).
 Рис. 4. «Компьютер». Модель задачи.
Рис. 4. «Компьютер». Модель задачи.
Таким образом, в процессе работы с наглядными пособиями ученики знакомятся с десятичным составом чисел от 11 до 19.
II. Сложение однозначных чисел с
переходом через десяток
1. Построение предметной модели задачи при помощи «Абака».
Чтобы не допустить "отлета математики от действительности" и обеспечить мотивацию путем распознавания в повседневной жизни проблем, требующих практического применения математических знаний, начнем работу с решения задачи. Например. Задача: «Хозяйка купила 7 помидоров и 5 огурцов. Сколько всего овощей купила хозяйка?» Условие задачи моделируется при помощи "Абака» (рис. 5).

Рис. 5. «Абак». Предметная модель задачи.
2. Построение ее графической, цветовой и знаковой модели с использованием «Компьютера» и ее преобразование, создание проблемной ситуации.
Учитель предлагает учащимся построить модель условия задачи при помощи полосок из персонального "Компьютера" (рис. 6, а). "Сколько овощей купила хозяйка?" – спрашивает он. Учащиеся затрудняются дать ответ сразу. Кто-то пересчитывает все овощи, кто-то присчитывает к 7 кружочкам 5 по одному.



а) б) в)
Рис. 6 (а, б, в,) «Компьютер». Построение и преобразование модели задачи.
Учитель создает условие для выполнения вычислений более рациональным способом. Он хочет поставить полоску с 5 кружочками в верхний карман «Компьютера» Она не входит, поэтому она накладывается на него. Учитель спрашивает: "Что можно сделать с числом 5, чтобы разместить в "Компьютере"?
И дети предлагают заменить его двумя полосками с 3 и 2 кружочками. Учитель ставит в верхний карман полоску с 3 кружочками, а в нижний – с 2 (рис. 6, в).
– Сколько овощей купила хозяйка? (12)
– Что мы сделали со II слагаемым?
– Заменили числами 3 и 2. Учитель обобщает: "Мы заменили II слагаемое – 5 суммой удобных слагаемых 3 и 2, чтобы 7 дополнить до 10, и прибавили 2.
Учащиеся моделируют эту же задачу на своих «Компьютерах» с проговариванием.
3. Построение знаковой модели при помощи «Линейки «Счет от 1 до 20».
Учитель на демонстрационном пособии "Линейка "Счет от 1 до 20" строит знаковую модель задачи (рис. 7).

Рис. 7. «Линейка «Счет от 1 до 20».
Знаковая модель задачи. Учащиеся строят эту же модель при помощи индивидуальных "Линеек "Счет от 1 до 20", сопровождая свои действия рассуждениями (хором): "Чтобы к 7 прибавить 5, надо к 7 прибавить 3, получится 10, (на линейке дана подсказка – удобное слагаемое 3), и к 10 прибавить 2, получится 12. Действия и рассуждения детей письменно оформляются на доске и в тетрадях в виде развернутой записи:
7 + 5 = 7 + (3 + 2) = (7 + 3) + 2 = 12
Таким образом, при последовательном использовании комплекса наглядных пособий формируется понятие о сложении однозначных чисел с переходом через десяток.
При формировании вычислительного навыка мы должны стремиться к свертыванию информации, т.е. избавиться от промежуточного результата 10, ибо он тормозит процесс вычислений. Поэтому фундаментом вычислительных навыков при сложении и вычитании однозначных чисел с переходом через десяток является знание состава чисел 11,12,…,18.
Алгоритм изучение состава чисел рассмотрим на примере числа 11.
III. Состав числа 11
1. Построение графической, цветовой и числовой модели состава числа 11.
Работа с демонстрационным и индивидуальным пособием «Компьютер». Для ограничения 10 кружков на доске нужно провести вертикальную линию, а на парту положить лист бумаги, ограничивающий десяток. В процессе совместной учебной деятельности строится модель числа 11. Учитель прикрепляет полоски при помощи магнитов и рядом записывает равенства, учащиеся размещают полоски на парте (рис. 8).
 Рис. 8. Развернутые модели состава числа 11.
Рис. 8. Развернутые модели состава числа 11.
Построение данных моделей позволяет за счет цвета и графики ярко и четко предъявить информацию и обеспечить переход от конкретного – к абстрактному.
2. Закрепление знаний. Самостоятельная работа в тетради.
Учащиеся в тетрадях по клеточкам вычерчивают карандашом модели числа 11 (рис. 9).
 Рис. 9. Запись в тетради.
Рис. 9. Запись в тетради.
Эта работа дает возможность акцентировать внимание на том, что I слагаемые уменьшаются на 1, а II - увеличиваются на 1, а сумма остается без изменения, и многократно повторить систематизированную информацию, что является необходимым условием запоминания таблицы сложения.
Полностью таблица представлена как справочный материал на правом клапане «Суперпапки».
Для закрепления состава числа 11 можно составить целую серию задач с использованием таблиц «Сказочный счет». Например. «В гости к героям сказки «Волк и семеро козлят» пришли герои сказки «Сестрица Аленушка и братец Иванушка». Сколько стало героев сказок?» (9 + 2 = 11) и т. д.
3. Применение полученных знаний на новых информационных полях и в новых ситуациях. Работа с демонстрационными пособиями «Радужная горка» и «Числовая горка».
На иллюстрации к сказке «Про Козленка, который умел считать до десяти" из комплекта "Сказочный счет" изображен парусник, на парусе которого шариками представлены числа от 1 до 10, а на корпусе – числа от 11 до 20.
Данную информацию можно использовать для закрепления знания состава числа. Работая в паре у доски, учащиеся устанавливают соответствие между а) парами шариков на парусе и числом 11 на корпусе парусника; б) парами шариков на парусе и парами чисел, составляющими число 11 в вертикальном столбике "Числовой горки".
Обращается внимание на то, что из всех чисел, расположенных между 1 и 10, объединив их в пары, можно получить число 11. Эту зависимость дети видели при изучении состава чисел первого десятка. 
Рис. 10.
На данном этапе было бы очень полезно составить задачи по моделям. Во-первых, мы замедлим темп урока, чтобы никто не отстал на самом важном этапе, а во-вторых, подключим воображение, фантазию, усилим ассоциативные связи.
Например.
1) В одной коробке лежало 9 простых карандашей, а в другой – 2 красных. Сколько карандашей в двух коробках?
2) Для приготовления баклажанной икры повар взял 8 баклажанов и 3 помидора. Сколько всего овощей пошло на баклажанную икру?
3) Для приготовления компота мама взяла 7 синих слив и 4 желтых. Сколько всего слив пошло на компот?
4. Взаимопроверка знаний. Работа в парах.
Учащиеся раскрывают "Суперпапку" и кладут ее на парту так, чтобы сверху были обе горки и клапан с таблицей сложения (рис. 11).
 Рис.11
Рис.11
1) Один ученик показывает кружочки: 9 серых и 2 красных кружочков, а другой – числа: 9 в сером квадрате и 2 в красном; 8 и 3 и т.д. Модели показываются сначала по порядку, а затем вперемешку. Проверяются по столбику выражений на клапане. Таким образом, они знакомятся с местом расположения данного столбика в системе знаний (рис. 10). Далее закрепление состава числа 11, обеспечивается переходом от абстрактного к конкретному, то есть от знаковой модели к предметной.
2) Один ученик показывает - 9 + 2, а другой – 9 серых шариков и 2 красных и т.д.
3) Один показывает на корпусе лодки число 11, а другой – на парусе 8 фиолетовых кружочков и 3 желтых и т.д.
5. Проверка знаний учителем. Игра "Сигнальщики".
На доске вывешивается "Цветовая сигнальная лента", в которой цвета радуги расположены по порядку, и рядом записываются соответствующие им числа, из которых можно составить число 11 – это 2, 3….9.
Учитель, например, показывает число 8 или фиолетовый цвет на ленте, а учащиеся – оранжевую карточку (3).
Итак, вся предыдущая работа была направлена на понимание и запоминание столбика таблицы сложения однозначных чисел с ответом 11, который является подсистемой в системе знаний.
Работа над составом чисел 12, 13….18 проводится аналогично.
Для проверки всей таблицы вывешивается "Цветовая сигнальная лента", в которой цвета радуги перемешаны, и рядом записываются по порядку числа 11, 12….18.
Учитель, например, называет выражение 5 + 9 (или показывает зеленую и серую карточку из веера).
Учащиеся видят, что число 14 написано рядом, например, с красным цветом и показывают красную карточку. (Цвет значения не имеет, он служит для обратной связи).
Можно придумать много других игр и заданий.
С огромным удовольствием дети работают с «Телефоном – справочником». Он же является самоучителем.
При помощи «Квадрата с уголком», благодаря подвижной детали, можно построить всю таблицу сложения и вычитания. Многочисленные варианты работы с каждым пособием, входящим в комплект, описаны в методических рекомендациях.
Эти учебно-наглядные пособия могут использоваться на всех этапах урока, в разных сочетаниях с другими средствами обучения, в том числе, и с учебником. Причем, детям предоставляется право выбирать наглядное пособие, при помощи которого можно выполнить то или иное задание из него.
